java的TreeMap使用的就是红黑树的实现， 现在很多厂面试的时候也会考这个问题，将自己的理解整理成文备忘，如果能帮助到你那么是我最大的快乐了

本文《红黑树概念深入浅出》由javacoder.cn整理， 转载请注明出处

网上有很多关于这个主题的文档，我觉得普林斯顿大学的red_black_tree.pdf是最深入浅出的。

红黑树的定义：
1、每个节点的颜色非红即黑
2、红色的节点不能相邻
3、从任一节点到叶子节点的所有路径中包含的黑节点数相同
4、根节点为黑节点（可以根据规则2和3推导出来， 如果根节点为红， 因为规则2那么加入的子节点只能为黑， 这时又不满足规则3，所以根节点只能为黑）

插入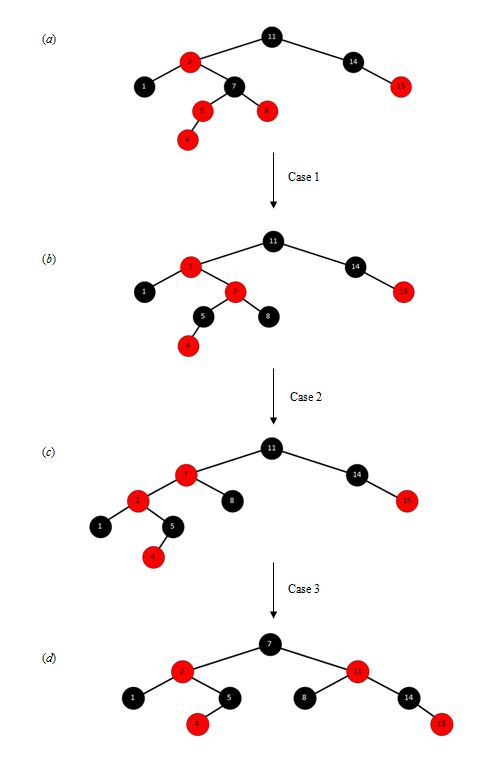

先找到待插入的位置，然后执行插入后的修复
分三种情况
a)case 1:如果当前元素的叔节点也为红色， 那么当前节点z->p，z->p->p->right与z->p->p节点颜色交互（当前节点的父节点、叔节点与祖父节点的颜色交换，这番操作后，z->p->p来看它的任意子树都是满足规则2和规则3的），然后z=z->p->p
b)case 2:如果不满足a),且当前节点是父节点的右子树， 那么对z->p执行左旋，且z=z->p 这番操作没有修复红黑树的任何规则，但是转化为了情况三
c)case 3:如果不满足a），且当前节点是父节点的左子树， 将z->p与z->p->p的颜色交换，然后对z->p->p执行右旋。

删除

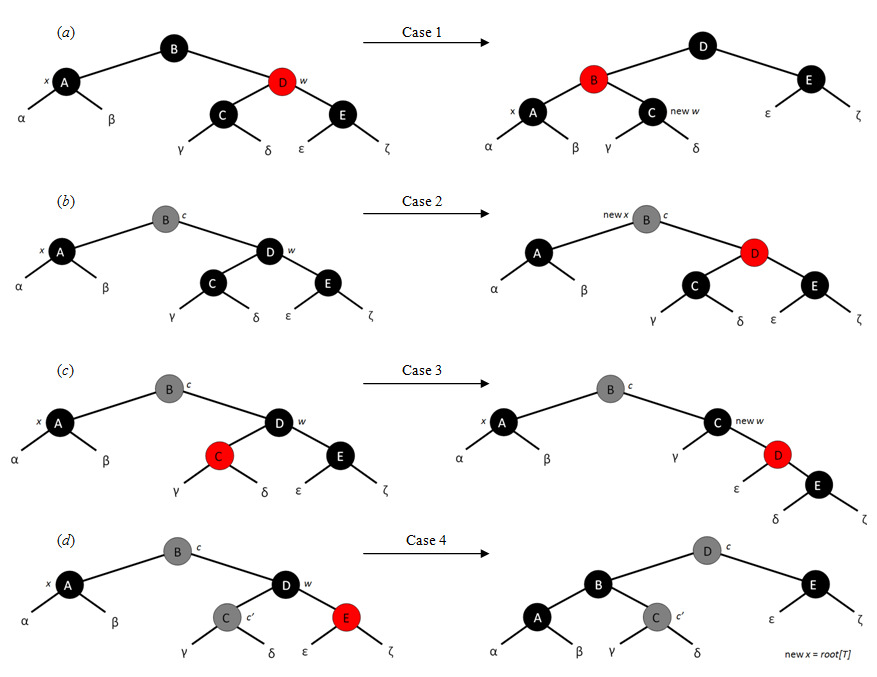
先找到待删除的元素，然后执行删除后的修复
对节点x删除不是进行节点删除后进行树的调整，而是将x的后继节点的值赋值给x， 然后删除x的后继节点
分4种情况
a)case 1: x的兄弟节点w为红色，将w和w->p的颜色互换，然后对w->p执行左旋。转换成case 2, case 3, case 4
b)case 2: x的兄弟节点w为黑色，且w的左右子节点也是黑色，直接将w涂上红色，也就是x的兄弟子树减少了一个黑节点，对于x->p 子树来说满足红黑树定义的，但是对于整棵红黑树来说不满足定义，因为x->p这棵子树减少了一个黑色的节点，所以赋值x=x->p，让当前节点上移一层继续调整。当然啦，如果当前x为红色， 那么直接将其涂成黑色，就完事了。
c)case 3:x的兄弟节点w为黑色，且w的右子节点也是黑色，将w和w-left子节点的颜色互换，然后对w执行右旋。变成case 4
d)case 4:x的兄弟节点w为黑色，且w的右子节点红色， 将w涂成w->p的颜色，然后w->p, w->right 涂成黑色， 最后对w->p执行左旋。调整完毕。

参考文档

Red/Black Tree 在线演示

Posted in: 面试加油站